第二章滚子轴承弹性线接触理论_泵阀轴承_资讯

第二章滚子轴承弹性线接触理论

2024-02-09 09:32 浏览:23

2.1 接触面接触半宽计算

按照Hertz接触理论，两个相当长且等长度的平行圆柱体接触时表面压力呈半椭圆柱分布，如图2.1和图2.2所示。各类滚子轴承一般均为线接触，表面压力可以认为近似呈半椭圆柱分布。须指出，各种球面滚子与滚道的接触面大小均按点接触计算，当接触椭圆长轴小于滚子长度时应力和变形也按点接触计算，当接触椭圆长轴大于滚子长度时应力和变形则按线接触计算。

(a) 圆柱滚子轴承 (b) 双圆柱接触模型
图2.1 双圆柱接触的等效模型

图2.2 理想线接触表面压力分布

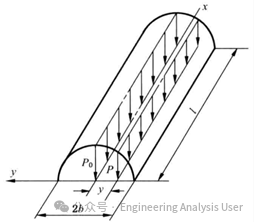
接触半宽可表示为：

式中，Q表示作用在轴承上的径向载荷，R₁表示滚子半径，R₂表示内圈滚道半径，l表示滚子等效接触长度和E′表示等效弹性模量。E′的表达式为：

式中，E₁，E₂，ν₁和ν₂分别表示滚子与滚道的弹性模量与泊松比。与滚道对应的滚子等效半径用R表示，其值取为：

2.2 接触区压应力与弹性趋近量计算

此外，滚动体与滚道之间接触特性还可采用有限元（FEM）方法进行计算分析，FEM模型如图2.3所示。

图2.3 滚子-滚道等效接触有限元计算模型

如图2.4为有限元等效模型计算的接触变形、接触应力与接触宽度。

2.3 接触刚度拟合方法

表2.1表示为两种计算方法的计算滚子与轴承内圈滚道接触的结果。表2.1结果表明，利用有限元模型建立的等效接触模型计算正常滚子与滚道接触，其结果与理想线接触计算方法的结果误差小，说明有限元模型有效。

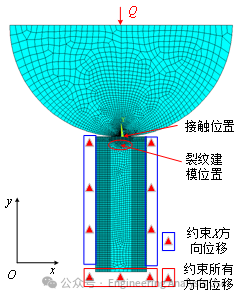
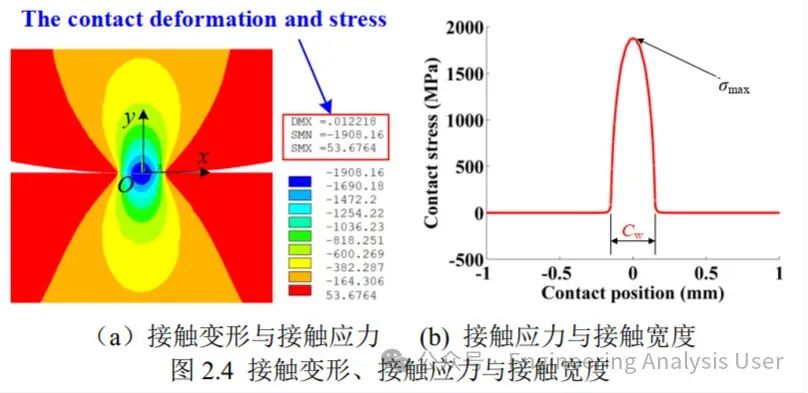
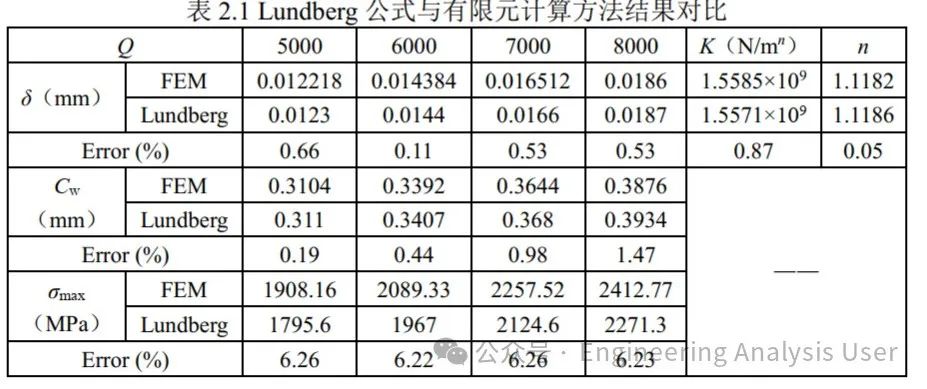2.4 MATLAB coding
Palmgren公式求刚度

clear;clc;format shortQ=100:100:1000;l=28.8;delta=3.84*1e-5*(Q.^0.9)./(l^0.8);Y=log(Q);X=log(delta);p=polyfit(X,Y,1);K=exp(p(2))*1000;n=p(1);K2=8.06e+4*(l)^(8/9)*1000;

参考文献：

[1] G. Lundberg, A. Palmgren. Dynamic capacity of rolling bearings[J]. Journal of Applied Mechanics 16 (2) (1949) 165-172.

[2] Hertz H. On the contact of elastic solids [J]. Journal of Reine and Angewandlte Mathematik, 1881, 92: 156-171.

备注：该章节代码编写简单，仅粘贴Palmgren公式及刚度拟合。

备注：下一章展示滚动轴承动力学建模方法。

打赏