☞ 这是金属加工（mw1950pub）发布的第17879篇文章

编者按

---

毛坯模型如图1所示。一般数控加工都是由上至下分层切削加工，因此毛坯上表面常常被设置为加工部分。毛坯模型上表面的网格离散非常重要。实际上，粗加工和精加工对毛坯模型表示精度有着不同的需求。粗加工的加工模型的表示精度要远低于精加工。因此，可以先构建一个较粗的网格作为粗加工的毛坯模型。具体方法如下。

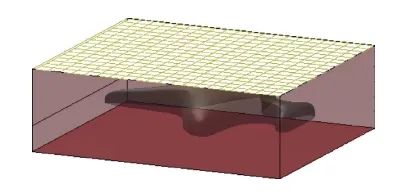
图1 毛坯模型

细分曲面初始控制网格，通过细分n次获得粗加工模型的极限网格，以d_s表示同一细分曲面面片中网格边的长度。进一步进行平均值计算。计算所求的平均值d_m即为粗加工毛坯上表面离散网格间距，具体计算公式为

式中，m表示精加工模型的细分次数，m>n。

粗加工仿真后，再将毛坯模型上表面细分（m-n）次，即可获得精加工毛坯模型。

3.1 遍历毛坯节点

如图2所示，毛坯上表面区域范围由大矩形表示，刀具扫描面区域范围由剖面线矩形表示。毛坯节点的几何坐标位于扫描面内部，表示方法为

x_max＋x_min）－（X_max＋X_min）≤（x_max－x_min）＋（X_max－X_min） （2）

（y_max＋y_min）－（Y_max＋Y_min）≤（y_max－y_min）＋（Y_max－Y_min） （3）

式中，X_max（X_min） 为毛坯顶点在X坐标轴向的最大（最小）坐标分量（mm）；Y_max（Y_min） 为毛坯顶点在Y坐标轴向的最大（最小）坐标分量（mm）；x_max（x_min）为刀具扫描面在X坐标轴向的最大（最小）坐标分量（mm）；y_max（y_min）为刀具扫描面在Y坐标轴向的最大（最小）坐标分量（mm）。

同理可得扫描面与毛坯不存在交集满足

（x_max＋x_min）－（X_max＋X_min）＞（x_max－x_min）＋（X_max－X_min）（4）

（y_max＋y_min）－（Y_max＋Y_min）＞（y_max－y_min）＋（Y_max－Y_min）（5）

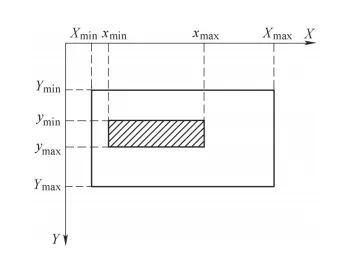
a）扫描面在毛坯内

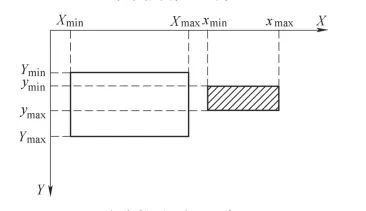
图2 毛坯节点与扫描面的关系

3.2 判断刀具扫描域

遍历毛坯节点后，分析毛坯节点与刀具扫描面（见图3）的位置关系。如果毛坯节点位于刀具扫描面内部，判断毛坯节点能否进行下一步的计算分析，主要依据是节点能否先后符合式（2）～式（5）的要求。

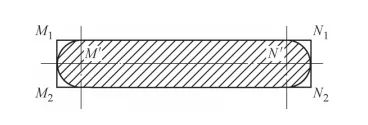
图3 毛坯节点与刀具扫描面

设两刀位点分别是M（X_M、Y_M、Z_M）和N（X_N、Y_N、Z_N），则以这两个刀位点为基础构成的X轴、Y轴以及Z轴的方向向量，分别可以用如下形式表示：a=X_N－X_M，b=Y_N－Y_M，c=Z_N－Z_M。由于以上3个方向向量具有对应的比例关系，依照此关系进一步分析研究可得

t＝[a（x－X_M）＋b（y－Y_M）＋c（z－Z_M）]/（a₂＋b₂＋c₂）（6）

当t＝0时，可判定刀位点M（X_M、Y_M、Z_M）与毛坯节点的几何坐标发生重叠；当t＝1时，代表刀位点N（X_N、Y_N、Z_N）与毛坯节点的几何坐标发生重叠。此时表明辅助坐标轴已经完成构建。

当t＝0时，表示辅助坐标轴的原点可以用M点表示，根据式（7）能够实现对原始坐标轴中的坐标进行转化，转化后的数值结果即为辅助坐标轴的三维坐标值。

3.3 切削毛坯节点位置计算

以环形铣刀为例获得刀具的扫描域形状，将扫描域分为若干部分来进行毛坯节点位置的数学表达。其他刀具同理。如图4所示，环形铣刀的刀具扫描域可以分为三部分：以M点和N点为分界，M点以左的区域表示为第一部分；M点和N点之间的区域表示为第二部分；N点以右的区域表示为第三部分。其中大径半圆的尺寸用R表示；小径半圆的尺寸用r表示，两半圆间的距离用R_c表示。以此可确定判断环形铣刀的刀具扫描域材料切削的数学表达式为

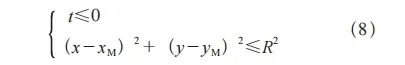
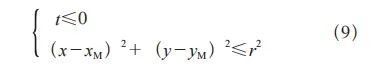
倘若点P符合式（9），可判定毛坯节点的几何坐标位于底面圆的内部区域，以此可确定变更P节点处在扫描面内的Z坐标，同时X坐标和Y坐标保持不变，计算公式为

Z＝Z_M－R_c                               （10）

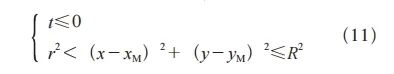
倘若P点符合式（11），即可判定毛坯节点处在圆环区域中。

当毛坯节点位于刀具扫描体内M点和N点之间的第二部分时，毛坯节点P（x、y、z）满足式（12）。中间部位可进一步分为两种情况：一是毛坯节点位于刀具扫描域的圆环区域内；二是毛坯节点位于刀具扫描域的矩形部位，即毛坯节点在刀具底部平面区域内。

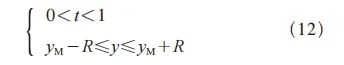
倘若P点符合式（13），可判定P点几何坐标处于加工刀具底面扫描域的区域内，则保持扫描面的X坐标和Y坐标不变的同时，进一步确定该毛坯节点P的Z坐标为

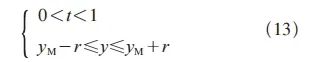
Z＝Z_M－R_c      （14）

倘若P点不能同时符合式（11）及式（13），可判定P点几何坐标处于刀具扫描域的圆环区域内，对刀具扫描体中四分之一球的圆心计算是此时的研究难点。依据式（15）可以实现对球心Ot（x_t、y_t、z_t）的计算

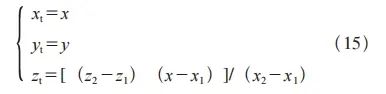
进而根据公式（16）得到z的值

（x－x_t）²＋（y－y_t）²＋（z－z_t）²＝R_c² （16）

倘若P（x、y、z）点符合式（17），可判定刀具扫描体位于刀具扫描域中N点以右的第三部分。依据环形铣刀的自身特点，毛坯节点的位置可进一步判定为两种情况：一是毛坯节点的位置处在圆环间的区域；二是毛坯节点位置处在环形铣刀平面圆内的区域。

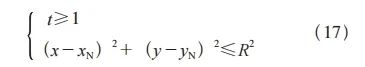
倘若P点符合式（18），可判定毛坯节点位置处在底部的平面圆区域内，保持扫描面毛坯节点P的X、Y坐标原数值，Z坐标修改为式（19）

Z=Z_M－R_c （19）

倘若P点符合式（20），可判定毛坯的节点几何坐标处在圆环的几何区域范围内，保持扫描面的X坐标和Y坐标原数值的同时，可依据环形铣刀圆角的公式模型进行计算，以此确定P点的Z坐标。

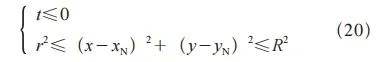
分析比较毛坯节点的z值以及式（19）计算得出的Z值。倘若Z<z时，将公式计算所求Z值赋值于毛坯节点的z值，即通过变更毛坯的z值来确定材料切削的情况。当加工刀具遍历过所有刀位点之后，最终实现切削加工仿真的完成。

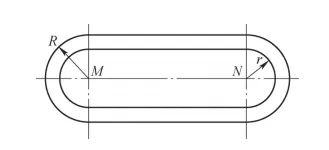
a）环形铣刀扫描域二维示意

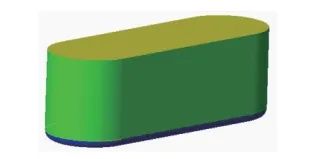
b）环形铣刀扫描域三维示意

图4 环形铣刀刀具扫描域

在加工模型上搜索毛坯模型顶点的最近距离点对是毛坯加工误差分析的基础。基于细分曲面多分辨力采样方法，可以实现最近距离点对的快速搜索。图5表示多分辨率采样搜索方法，其中正方形表示择优点；黑色圆点表示采样点。最后在黑色区域择优选取最近点，其所在的空间范围为下次采样范围。

因此择优点可表示为

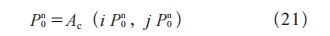
式中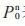，表示第n次选取的择优点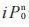；表示择优点的行索引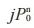；代表择优点的列索引。

对于第n次搜索的4个采样点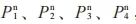，第n‒1次择优点索引值为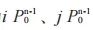，则可以得到从第2次到第n－1次获得采样点的公式

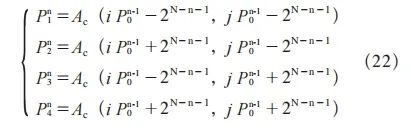
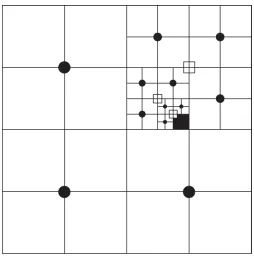
图5 多分辨率采样搜索方法

采用图6所示的细分曲面模型作为加工模型，粗加工采用环形铣刀；半精加工和精加工采用球头铣刀对加工模型进行数控加工试验。粗加工、半精加工和精加工阶段的刀具轨迹如图7所示。各加工阶段的加工仿真和加工试验结果如图8所示。

图6 加工模型

a）粗加工 b）半精加工 c）精加工

图7 3个加工阶段的刀具轨迹

a）粗加工仿真 b）粗加工试验

c）半精加工仿真 d）半精加工试验

图9 加工误差分析色图

利用细分曲面多分辨率采样方法，实现了最近距离点对的快速搜索。该方法为加工仿真的快速实现和误差分析的高效计算奠定了基础。

[1] REIF U. A unified approach to subdivision algorithmsnear extraordinary vertices[J]. Computer AidedGeometric Design， 1995， 12（2）：153-174.

[2] SPENCE A，ALTINTAS Y， KIRKPATRICK D.Direct calculation of machining pararmeters from asolid model[J]. Computers in Industry，1990，14（4）：271-280.

[3] HUNT W A，VOELCKER H B. An exploratory studyof automatic verification of programs for numericallycontrolled machine tools[M]. N.Y：Rochester，1982.

[4] SU C，LIN F，YE L. A new collision detectionmethod for CSG-represented objects in virtualmanufacturing[J]. Computers in Industry，1999（40）：1-13.

[5] BRAID I C. Designing with Volumes[M]. London：University of Cambridge，1973.

[6] FLEISIG R V，SPENCE A D. Techniques foraccelerating B-rep based parallel machiningsimulation[J]. Computer-Aided Design，2005， 37（12）：1229-1240.

[7] CHAPPEL I T. The use of vectors to simulate materialremoved by numerically controlled milling[J].Computter-Aided Design，1983， 15（3）：156-158.

[8] WANG W P， WANG K K. Geometric modeling forswept volume of moving solids[J]. IEEE ComputerGraphics and Applications， 1986， 6（12）：8-17.

[9] VAN HOOK T. Real-time shaded NC millingdisplay[J]. Computer Graphics，1986，20（4）：15-20.

[10] CHANG K，GOODMAN E. A method of NCtoolpath interference detection for a multi-axismachining system[J]. Control of ManufacturingProcesses，1991，11（5）：23-30.

-End-

☞来源：金属加工 ☞编辑：王瑞艳  ☞责任校对：邵玉洁 ☞审核人：吴晓兰 ☞媒体合作: 010-88379790-801 ☞金属加工杂志唯一投稿网址：http://tougao.mw1950.cn/