机械原理知识点大全
2024-02-19 09:33 浏览:44
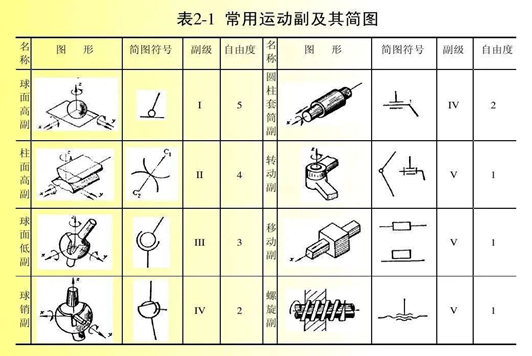
基本概念:机器、机构、机械、零件、构件、机架、原动件和从动件。机构运动简图的绘制、运动链成为机构的条件和机构的组成原理是本章学习的重点。为保证机构运动简图与实际机械有完全相同的结构和运动特性,对绘制好的简图需进一步检查与核对(运动副的性质和数目来检查)。运动链成为机构的条件是:原动件数目等于运动链的自由度数目。机构自由度的计算错误会导致对机构运动的可能性和确定性的错误判断,从而影响机械设计工作的正常进行。准确识别复合铰链、局部自由度和虚约束,并做出正确处理。复合铰链是指两个以上的构件在同一处以转动副相联接时组成的运动副。正确处理方法:k个在同一处形成复合铰链的构件,其转动副的数目应为(k-1)个。 局部自由度是机构中某些构件所具有的并不影响其他构件的运动的自由度。局部自由度常发生在为减小高副磨损而增加的滚子处。 正确处理方法:从机构自由度计算公式中将局部自由度减去,也可以将滚子及与滚子相连的构件固结为一体,预先将滚子除去不计,然后再利用公式计算自由度。虚约束是机构中所存在的不产生实际约束效果的重复约束。正确处理方法:计算自由度时,首先将引入虚约束的构件及其运动副除去不计,然后用自由度公式进行计算。虚约束都是在一定的几何条件下出现的,这些几何条件有些是暗含的,有些则是明确给定的。对于暗含的几何条件,需通过直观判断来识别虚约束;对于明确给定的几何条件,则需通过严格的几何证明才能识别。机构的组成过程和机构的结构分析过程正好相反,前者是研究如何将若干个自由度为零的基本杆组依次联接到原动件和机架上,以组成新的机构,它为设计者进行机构创新设计提供了一条途径;后者是研究如何将现有机构依次拆成基本杆组、原动件及机架,以便对机构进行结构分类。 1.基本概念:速度瞬心、绝对速度瞬心和相对速度瞬心(数目、位置的确定),以及“三心定理”。 3.同一构件上两点的速度之间及加速度之间矢量方程式、组成移动副两平面运动构件在瞬时重合点上速度之间和加速度的矢量方程式,在什么条件下,可用相对运动图解法求解? 5. 构件的角速度和角加速度的大小和方向的确定以及构件上某点法向加速度的大小和方向的确定。 6.哥氏加速度出现的条件、大小的计算和方向的确定。“静力分析”、“动力分析”及“动态静力分析” 、“平衡力”或“平衡力矩”、 “摩擦角”、“摩擦锥”、 “当量摩擦系数”和“当量摩擦角”(引入的意义)、“摩擦圆”。根据两构件之间的相对运动(或相对运动的趋势)方向,正确地确定总反力的作用方向是本章的难点之一。移动副(斜面摩擦、槽面摩擦):总反力Rxy总是与相对速度vyx 之间呈90°+φ的钝角;槽面摩擦问题可通过引入当量摩擦系数及当量摩擦角的概念,将其简化为平面摩擦问题。运动副元素的几何形状不同,引入的当量摩擦系数也不同,由此使得运动副元素之间的摩擦力不同。转动副:总反力Rxy总是与摩擦圆相切。它对铰链中心所形成的摩擦力矩Mfxy=Rxy·ρ。方向与相对角速度ωyx的方向相反。Rxy的确切方向需从该构件的力平衡条件中得到。2.“机构效率”和“损失系数”以及具体机构效率的计算方法。3.“自锁”与“不动”这两个概念有何区别?“不动”的机构是否一定“自锁”?机构发生自锁是否一定“不动”?为什么?无论驱动力多大,机械都无法运动的现象称为机械的自锁。其原因是由于机械中存在摩擦力,且驱动力作用在某一范围内。一个自锁机构,只是对于满足自锁条件的驱动力在一定运动方向上的自锁;而对于其他外力,或在其他运动方向上则不一定自锁。因此,在谈到自锁时,一定要说明是对哪个力,在哪个方向上自锁。1)对移动副,驱动力位于摩擦角之内;对转动副,驱动力位于摩擦圆之内。2) 令工作阻力小于零来求解。采用图解解析法或解析法求出工作阻力与主动力的数学表达式,然后再令工作阻力小于零,即可求出机构的自锁条件。根据直径D与轴向宽度b之比的不同,刚性转子可分为两类:(1) 当b / D≤0.2时,可以将转子上各个偏心质量近似地看作分布在同一回转平面内,其惯性力的平衡问题实质上是一个平面汇交力系的平衡问题。(2) 当b / D >0.2时,转子的轴向宽度较大,首先应在转子上选定两个可添加平衡质量的、且与离心惯性力平行的平面作为平衡平面,然后运用平行力系分解的原理将各偏心质量所产生的离心惯性力分解到这两个平衡平面上。这样就把一个空间力系的平衡问题转化为两平衡平面内的平面汇交力系的平衡问题。当b / D≤0.2时,可在平衡架上进行静平衡试验。当b / D >0.2时,则需要在动平衡机上进行动平衡试验。第七章 机械的运转及其速度波动的调节
本章主要研究两个问题:一是确定机械真实的运动规律;二是研究机械运转速度的波动调节。机械在外力作用下的运转过程分为启动、稳定运转和停车等3个阶段。注意理解3个阶段中功、能量和机械运转速度的变化特点。(1) 对于单自由度的机械系统,研究机械的运转情况时,可以就某一选定的构件(即等效构件)来分析,将机械中所有构件的质量、转动惯量都等效地转化到这一构件上,把各构件上所作用的力、力矩也都等效地转化到等效构件上,然后列出等效构件的运动方程式来研究其运动规律。这就是建立所谓的等效动力学模型的过程。(2) 建立机械系统等效动力学模型时应遵循的原则是:使机械系统在等效前后的动力学效应不变,即① 动能等效:等效构件所具有的动能,等于整个机械系统的总动能。② 外力所做的功等效:作用在等效构件上的外力所做的功,等于作用在整个机械系统中的所有外力所做功的总和。(1) 周期性速度波动的机械系统,可以利用飞轮储存能量和释放能量的特性来调节机械速度波动的大小。飞轮的作用就是调节周期性速度的波动范围和调节机械系统能量。(2) 非周期性速度波动的机械系统,不能用飞轮进行调节。当系统不具有自调性时,则需要利用调速器来对非周期性速度波动进行调节。(1) 飞轮设计的基本问题,是根据等效力矩、等效转动惯量、平均角速度,以及机械运转速度不均匀系数的许用值来计算飞轮的转动惯量。无论等效力矩是哪一种运动参数的函数关系,最大盈亏功必然出现在ωmax和ωmin所在两位置之间。① 为减小飞轮转动惯量(即减小飞轮的质量和尺寸),应尽可能将飞轮安装在系统的高速轴上。② 安装飞轮只能减小周期性速度波动,但不能消除速度波动。第八章 平面连杆机构及其设计
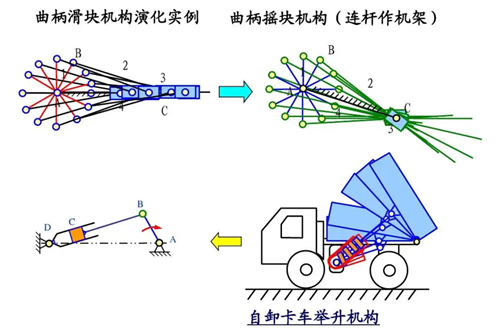
铰链四杆机构可以通过4种方式演化出其他形式的四杆机构:①取不同构件为机架;有时某一机构本身并无急回特性,但当它与另一机构组合后,此组合后的机构并不一定亦无急回特性。机构有无急回特性,应从急回特性的定义入手进行分析。压力角是衡量机构传力性能好坏的重要指标。对于传动机构,应使其α角尽可能小(γ尽可能大)。连杆机构的压力角(或传动角)在机构运动过程中是不断变化的,在从动件的一个运动循环中,α角存在一个最大值αmax。在设计连杆机构时,应注意使αmax≤[α]。此处应注意:“死点”、“自锁”与机构的自由度F≤0的区别。自由度小于或等于零,表明该运动链不是机构而是一个各构件间根本无相对运动的桁架;死点是在不计摩擦的情况下机构所处的特殊位置,利用惯性或其他办法,机构可以通过死点位置,正常运动;自锁是指机构在考虑摩擦的情况下,当驱动力的作用方向满足一定的几何条件时,虽然机构自由度大于零,但机构却无法运动的现象。死点、自锁是从力的角度分析机构的运动情况,而自由度是从机构组成的角度分析机构的运动情况。3. 平面连杆机构的设计(曲柄摇杆机构、曲柄滑块机构、导杆机构)平面连杆机构运动设计常分为三大类设计命题:刚体导引机构的设计、函数生成机构的设计和轨迹生成机构的设计。在设计一个四杆机构使其两连架杆实现预定的对应角位置时,可以用 “刚化反转法”求解此四杆机构。这个问题是本章的难点之一。第九章 凸轮机构及其设计
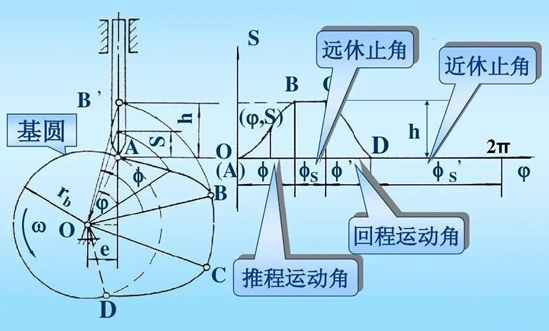
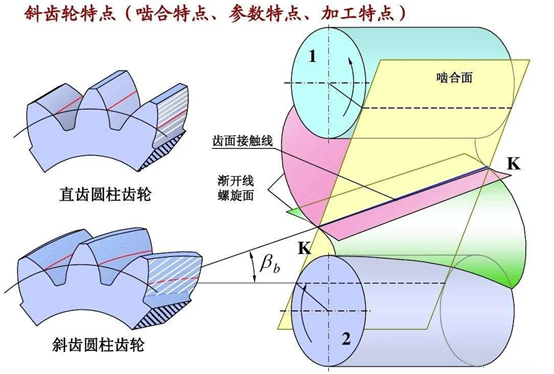
a:名词术语:推(回)程运动角、远(近)休止角、推程、基圆等。b:常用的运动规律:方程式的推导(仅要求等速)、运动线图及其变化规律、运动特点(刚(柔)性冲击及其发生的位置、时刻和应用的场合)。c:运动规律的选择依据:满足工作对从动件特殊的运动要求;满足运动规律拼接的边界条件,即各段运动规律的位移、速度和加速度值在连接点处应分别相等;使最大速度和最大加速度的值尽可能小。无论是用图解法还是解析法设计凸轮廓线,所依据的基本原理都是反转法原理。a:压力角:定义、不同位置时机构压力角的确定以及对压力角所提出限制的原因(αmax不超过许用压力角[α])确定原则:αmax≤α或者ρmin≥[ρ]=3~5 mmc:滚子半径:取决于凸轮轮廓曲线的形状,对于内凹的曲线形状,保证最大压力角αmax不超过许用压力角[α];对于外凸的曲线形状,保证凸轮实际廓线的最小曲率半径ρa min= ρmin-rr ≥ 3~5 mm,以避免运动失真和应力集中。运动失真:增大基圆半径、减小滚子半径以及改变机构的运动规律。在设计移动滚子从动件盘形凸轮机构时,若发现其压力角超过了许用值,可以采取以下措施:(2) 选择合适的从动件偏置方向。在设计凸轮机构时,若发现采用对心移动从动件凸轮机构推程压力角过大,而设计空间又不允许通过增大基圆半径的办法来减小压力角时,可以通过选取从动件适当的偏置方向,以获得较小的推程压力角。即在移动滚子从动件盘形凸轮机构的设计中,选择偏置从动件的主要目的,是为了减小推程压力角。(2) 当采用滚子从动件时,滚子半径必须小于凸轮理论廓线外凸部分的最小曲率半径ρmin,通常取rr≤0.8ρmin。若由于结构、强度等因素限制,rr不能取得太小,而从动件的运动规律又不允许修改时,则可通过加大凸轮的基圆半径rb,从而使凸轮廓线上各点的曲率半径均随之增大的办法来避免运动失真。对于移动平底从动件盘形凸轮机构来说,偏距e并不影响凸轮廓线的形状,选择适当的偏距,主要是为了减轻从动件在推程中过大的弯曲应力。本章的特点是名词、概念多,符号、公式多,理论系统性强,几何关系复杂。学习时要注意清晰掌握主要脉络,对基本概念和几何关系应有透彻理解。(8) 齿轮齿条啮合传动与标准齿条型刀具范成加工齿轮2. 什么是节点、节线、节圆以及齿廓啮合基本定律?定传动比的齿廓曲线的基本要求?3. 渐开线齿廓:形成、特性以及其在传动过程中的优点。4. 标准齿轮:概念、名称符号、基本参数以及几何尺寸。5. 渐开线直齿圆柱齿轮的正确啮合条件、安装条件和连续啮合传动条件。6. 标准齿轮的标准安装中心距,标准安装有什么特点;非标准安装中心距,非标准安装有什么特点。加工标准齿轮的条件、轮齿齿廓的根切(定义、条件以及不发生根切的最少齿数Zmin。变位修正法:为了切制齿数少于17且不发生根切的齿轮、在无齿侧间隙的条件下拼凑中心矩以及改善传动性能(强度性能和啮合性能)所采用的改变刀具与轮坯相对位置的加工方法。变位齿轮:正变位、负变位齿轮的概念以及与标准齿轮的尺寸差别。8. 斜齿轮:渐开线螺旋曲面齿廓的形成、基本参数(端面与法面参数的关系)以及几何尺寸的计算。9. 斜齿轮传动:正确啮合条件、中心矩条件和连续传动条件。10. 斜齿轮的当量齿轮和当量齿数:概念、意义和作用。11. 直齿圆锥齿轮:基本参数和尺寸特点。圆锥齿轮传动的背锥、当量齿轮、当量齿数。虽然定轴轮系的传动比计算最为简单,但它却是本章的重点内容之一。定轴轮系传动比的大小,等于组成轮系的各对啮合齿轮中从动轮齿数的连乘积与主动轮齿数的连乘积之比,关于定轴轮系中主、从动轮转向关系的确定有3种情况。(1) 轮系中各轮几何轴线均互相平行:在这种情况下,可用(-1)m来确定轮系传动比的正负号,m为轮系中外啮合的对数。(2) 轮系中齿轮的几何轴线不都平行,但首末两轮的轴线互相平行:仍可用正、负号来表示两轮之间的转向关系:二者转向相同时,在传动比计算结果中标以正号;二者转向相反时,在传动比计算结果中标以负号。需要特别注意的是,这里所说的正负号是用在图上画箭头的方法来确定的,而与(-1)m无关。(3) 轮系中首末两轮几何轴线不平行:首末两轮的转向关系不能用正、负号来表示,而只能用在图上画箭头的方法来表示。周转轮系传动比计算的基本思路:假想给整个轮系加上一个公共的角速度(-ωH),使系杆固定不动,将周转轮系转化成一个假想的定轴轮系再进行传动比或者运动参量的求解。混合轮系传动比计算既是本章的重点,也是本章的难点。混合轮系传动比计算的基本思路:首先,将各个基本轮系正确地划分开来,分别列出计算各基本轮系传动比的关系式,然后找出各基本轮系之间的联系,最后将各个基本轮系传动比关系式联立求解。第十二章 其它常用机构及其设计
本章的重点是掌握各种常用间歇运动机构(棘轮机构、槽轮机构、螺旋机构和万向铰链机构)的工作原理、结构组成、运动特点和功能,并了解其适用的场合,以便在进行机械系统方案设计时,能够根据工作要求正确地选择执行机构的型式。