孩子们升入二年级了。

在一年级“听、说、读、写”四项基本功训练的基础上开展思维能力的初步培养后，随着孩子们识字量的逐步增加，二年级开始计划重点培养学生阅读数学书的能力和以讲述为主要外显表现形式的思维能力。

上周在课余的游戏时间，我给任教的两个班级的孩子们分别提出了同一个思考问题：

在我初步讲述这个数学故事的含义后，我请同学们用自己的话说说这个故事说了什么，问了什么问题。通过孩子们的表达，可以看得出他们都理解了这个故事。

在其中的一个班级，我请小朋友们自己利用课余时间独立思考，也不急于让他们得出答案。不过没过一会儿，这个班级的一位小朋友就给我看了她画的图。

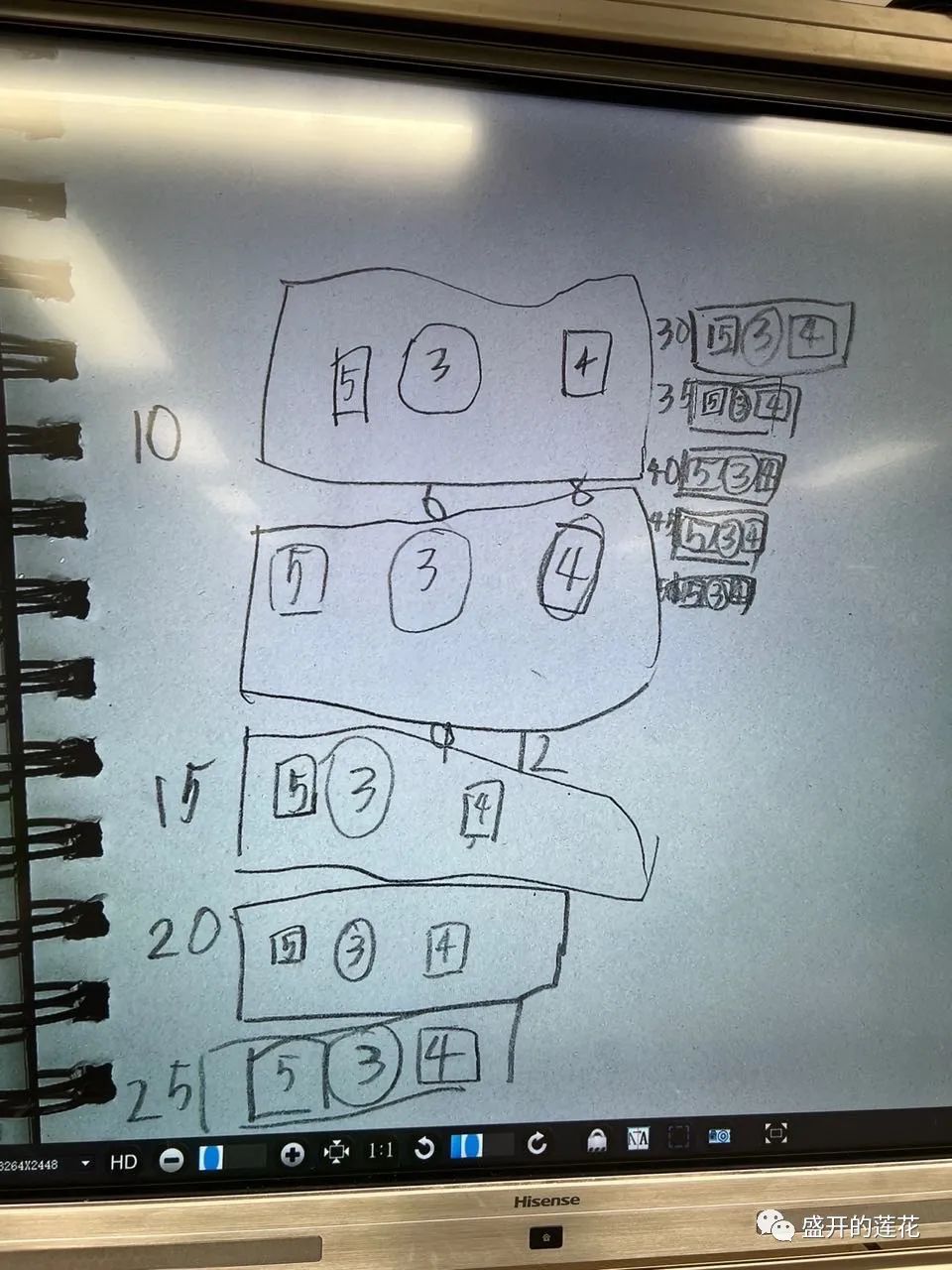
我请她解释，她也没能说的特别清楚。我只是问她，那么现在能装成几个礼盒？什么东西用完了？其他东西还有剩余吗？并不急于让她回答我。

过了两天，在我担任另一个班级的课后服务的看班老师的时间段里，我把前几天提出的这个数学故事和问题请小朋友说一说他们对这个问题思考的怎么样了？

十余位孩子纷纷举手。

我宣布了分享规则：每人最多可以发言三分钟，在这三分钟里，既可以使用实物投影，也可以使用粉笔，老师只担任发言同学的助教，同学们负责听他的发言，并思考是否听得懂，如果自己上来讲，哪里是需要改进的。

孩子们按照举手的顺序，一一上来分享自己的思考。

不过这次，出现了一些问题：首先第一位同学写的字非常小，经过改进，第二位同学字就变大了。第二位同学使用了“未来要学习的知识——除法”，而且，显然，使用的不正确，同学们也听不懂，他自己说到一半也说不下去了。我表扬了孩子的大方发言。也提出“我们要使用目前学习过的知识，尽量不用“未来的知识””。第三位，第四位，第五位……我在孩子的回答上看到了每位孩子积极思考的态度和乐于分享的热情，还看到了一位位隐身其后的父母长辈的殷殷辅导。这一切都令我这个做老师的非常高兴与感动。

但是，这十位左右的孩子，基本都是说到一半说不下去，或者是按照自己记录在笔记本上的思考过程，先是说，但说到后来，自己显然也思路不畅，只能照本宣科地读完。

这是我们二年级的孩子第一次就一个较复杂的数学问题进行长时间思考后的整段完整逻辑表达练习。能有积极分享的过程就是一个很好的开始。

那么为什么孩子的思路会呈现趋同的障碍，怎样帮助孩子形成自己的思维过程，能进行流畅的逻辑推理表达呢？

首先，这个思考问题的过程必须是自己本人主动思考参与的。

为什么第一位孩子仅仅在课堂上，用时不久就采用画图的方法，走在正确的思考路线上？

更大的原因是孩子自己的独立主动思考。尽量不受外界的过多杂音的影响。

“画图”是一个非常有用的帮助思考的工具。在一年级我们就学习如何使用画图帮助思考。因此遇到较复杂的问题时，采用画图的方法，就能够在这个“问题毛线球”中找到一根线头，顺着这个线头，就能拆开这个“问题毛线球”。

其次，化繁为简，从简单入手的思考方法，是孩子们需要不断体会和实践的。

在“找次品”这个内容的学习中，例题是：243个零件中，有1个次品，这个次品的质量比正品的质量略轻，现在有一架天平秤，请问至少称量几次，可以找到这个次品？

这是一个模型化的问题，但是在找到解题模型之前，如果直接介绍这个模型，那思维一定是不可持续发展的，也难以做到举一反三，推而广之。

因此教学中，是从2个零件有1个次品，3个零件有1个次品，4个零件有1个次品，5个零件有1个次品……在简单问题情境中，不断地找方案，然后归纳方案中的共同部分，从而最终形成“一分为三”的数学模型。

如果孩子们真实经历了这个探索的过程，那么题目变化，孩子们也能够学会“从简化问题开始寻找解答方案”这个方法。

第三，过早介绍使用现成工具，不利于孩子的能力发展。

拿刚才的例子来说，如果一开始就告诉他们“把243平均分成三份，先秤其中的2份”。孩子一定会不明就里。当我们直接告诉孩子在这个问题中，天平秤一次，就可以比出3份的轻重。他们一定也不明白为什么。只有让他们自己从2个，3个，4个逐步秤，经历称和思考归纳的过程，才能感悟到“三”的含义。

拿分礼盒这个问题来说，我们成年人经历了十数年的学习，积累了丰富的学习经验。我们已经完全明白乘法，除法，余数等含义。如果我们就告诉孩子用乘法，或者用除法，孩子在没有经历完整推理过程，直接使用工具，也会产生工具使用不当，不明白为什么用，怎么用的现象。

以培养思维能力为第一目标的教学应该采用第一性原理。一层一层地拨开事物的表象，看到其中的本质，再从本质一层一层地往上走。可以说只有找到解决问题的第一性原理，在能看清问题的本质，从而从根本上理解问题，解决问题，达成目标。而不是沿着已经归纳好的流程做。也不知道这个流程适不适合。究竟流程是我们的主人，还是我们是流程的主人？

纵观人类认识世界的过程，乘法是从解决加法问题的现实需要中发展而来，除法是在解决减法问题的现实需要中发展而来的。对于个体而言，他们认识世界的过程其实就是遵循着人类认识世界的发展进程。虽然会伴随着现代教育的推进和引导，能够极大地缩短这个过程的时间跨度，但关键节点，个体是必须要一一经历的。个体不经历这个认知发展的每一个重要节点过程，就无法形成自己认知世界的真正能力。


第四、思考的过程重于问题答案，养成“苦思冥想”，学会享受思考的乐趣，不急于求成，是优秀的学习品质，也是孩子们今后探索未知世界的动力之源。

不急于求成，是一个听让现代人抓狂的要求。从电子游戏，到app评价，现在的社会，现代的技术，无一不在提供即时反馈，通过即时反馈抓住流量，抓住用户，激励各种商业需要的购买行为，引导各种行为的持续或者中止。

但是数学研究就像一株植物，需要在时间的厚土中慢慢生长。待到成果之花绽放的那一刻，便是“啊哈时刻”，是“尤里卡时刻”。

费马大定理的数学家安德鲁·怀尔斯（Andrew Wiles）打过一个比方。他说钻研数学就好像是在一个全黑的房间里摸索。你根本没有固定的线路，只是到处摸，终于有一天你摸到了房间的开关，你按下去，整个房间一下子就亮了，你豁然开朗。接着你再到第二个房间去摸索，又不知道过了多长时间，才找到第二个开关……怀尔斯说灯光亮起来那一瞬间的喜悦和兴奋，是任何感觉都无法相比的。

所以，引领孩子经历探索发现的过程，放慢脚步，享受学习，体会收获的快乐。在对原发思考的鼓励中，孩子的思维能力才会一步一步提升。