еүҚиЁҖ
иҪҙжүҝеҶ…йғЁй—ҙйҡҷжҳҜеӨ–еңҲе’ҢеҶ…еңҲеңЁзӣёеҸҚж–№еҗ‘жҺЁеҠӣгҖҒзӣёеҜ№иҝҗеҠЁж—¶дә§з”ҹзҡ„й—ҙйҡҷгҖӮжІҝзӣҙеҫ„ж–№еҗ‘зҡ„移еҠЁжҳҜеҫ„еҗ‘й—ҙйҡҷпјҢиҖҢжІҝиҪҙж–№еҗ‘зҡ„移еҠЁеҲҷжҳҜиҪҙеҗ‘й—ҙйҡҷгҖӮ
з”ұдәҺеӨҡз§ҚеҺҹеӣ пјҢеҶ…йғЁй—ҙйҡҷеҜ№иҪҙжүҝзҡ„дҪҝз”ЁжҖ§иғҪиҮіе…ійҮҚиҰҒгҖӮй—ҙйҡҷзҡ„еӨ§е°ҸдјҡеҪұе“ҚиҪҙжүҝдёӯзҡ„иҪҪиҚ·еҲҶеёғпјҢиҖҢиҪҪиҚ·еҲҶеёғжңҖз»ҲдјҡеҪұе“ҚеҲ°иҪҙжүҝиҝҗиЎҢеҷӘйҹігҖҒжҢҜеҠЁеҸҠиҪҙжүҝзҡ„дҪҝз”ЁеҜҝе‘ҪгҖӮжӯӨеӨ–пјҢиҪҪиҚ·еҲҶеёғеҸҜиғҪиҝҳдјҡеҪұе“ҚеҲ°иҪҙжүҝзҡ„ж»ҡеҠЁе…ғ件жҳҜйҖҡиҝҮж»ҡеҠЁиҝҗеҠЁиҝҳжҳҜж»‘еҠЁиҝҗеҠЁжқҘ移еҠЁгҖӮ
йҖҡеёёпјҢиҪҙжүҝзҡ„еҶ…еңҲжҲ–еӨ–еңҲеқҮйҮҮз”ЁиҝҮзӣҲй…ҚеҗҲе®үиЈ…гҖӮиҝҷдјҡеҜјиҮҙиҶЁиғҖпјҲеҶ…еңҲпјүжҲ–收缩пјҲеӨ–еңҲпјүпјҢд»ҺиҖҢеҜјиҮҙз»„иЈ…иҝҮзЁӢеҗҺиҪҙжүҝзҡ„еҶ…йғЁй—ҙйҡҷеҸ‘з”ҹеҸҳеҢ–гҖӮеҪ“жңәз»„иҝҗиЎҢж—¶пјҢиҪҙжүҝзҡ„е·ҘдҪңжё©еәҰйҖҡеёёеҸҜиғҪдјҡеҚҮй«ҳпјҢзӣҙеҲ°иҫҫеҲ°йҘұе’Ңжё©еәҰпјҢжӯӨж—¶зі»з»ҹзҡ„дә§зғӯе’ҢжҺ’зғӯиҫҫеҲ°е№іиЎЎгҖӮ
иҷҪ然жҲ‘们йҖҡеёёе°ҶжӯӨйҖҡз”Ёе·ҘдҪңжё©еәҰз”ЁдәҺж•ҙдёӘиҪҙжүҝпјҢдҪҶеҶ…еңҲгҖҒеӨ–еңҲе’Ңж»ҡеҠЁе…ғ件зҡ„е®һйҷ…жё©еәҰеҸҜиғҪдјҡжңүеҫҲеӨ§е·®ејӮгҖӮ
иҝҷз§Қжё©е·®еҸҜиғҪдјҡеҜјиҮҙеҶ…йғЁй—ҙйҡҷеҸ‘з”ҹеҸҳеҢ–пјҢеҰӮеӣҫ1жүҖзӨәгҖӮжӯӨеӨ–пјҢеҪ“иҪҙжүҝеңЁиҙҹиҪҪдёӢиҝҗиЎҢж—¶пјҢеҶ…еңҲгҖҒеӨ–еңҲе’Ңж»ҡеҠЁе…ғ件зҡ„еј№жҖ§еҸҳеҪўд№ҹдјҡеҜјиҮҙй—ҙйҡҷзҡ„еҸҳеҢ–гҖӮйҮҸеҢ–жүҖжңүиҝҷдәӣеҸҳеҢ–дјҡдҪҝи®Ўз®—иҪҙжүҝеҶ…йғЁй—ҙйҡҷжҲҗдёәдёҖйЎ№еӨҚжқӮзҡ„д»»еҠЎгҖӮд»ҘдёӢжҳҜй—ҙйҡҷзұ»еһӢзҡ„е®ҡд№үгҖӮ
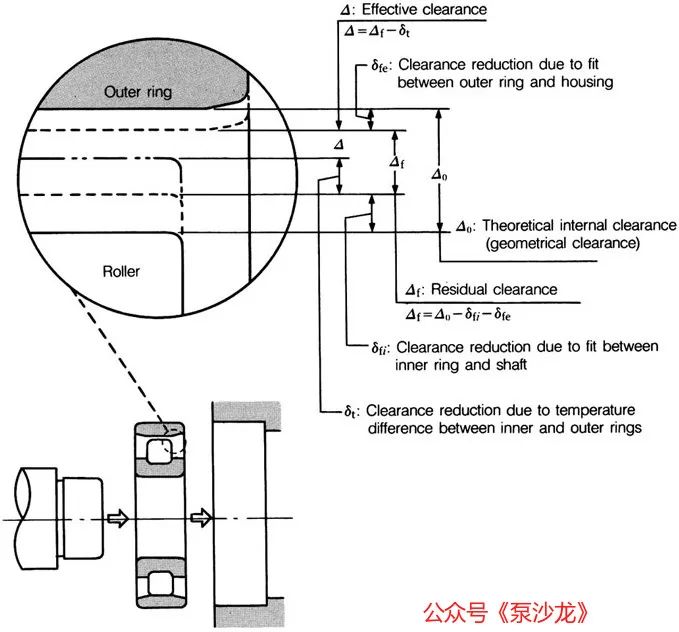
еӣҫ1пјҡеңҶжҹұж»ҡеӯҗиҪҙжүҝеҫ„еҗ‘еҶ…йғЁй—ҙйҡҷзҡ„еҸҳеҢ–пјҲеӣҫзүҮз”ұNSKжҸҗдҫӣпјү
жөӢйҮҸзҡ„еҶ…йғЁй—ҙйҡҷпјҲвҲҶ1пјү
иҝҷжҳҜеңЁи§„е®ҡзҡ„иҙҹиҪҪдёӢжөӢйҮҸзҡ„еҶ…йғЁй—ҙйҡҷпјҢеҸҜд»Ҙз§°дёәвҖңиЎЁи§Ӯй—ҙйҡҷвҖқгҖӮиҝҷдёӘй—ҙйҡҷеҢ…жӢ¬иҙҹиҪҪеј•иө·зҡ„еј№жҖ§еҸҳеҪўпјҲПғFOпјүгҖӮ
вҲҶ1В = вҲҶ0В + ПғFO
зҗҶи®әеҶ…йғЁй—ҙйҡҷпјҲвҲҶ0пјү
иҝҷжҳҜеҫ„еҗ‘еҶ…йғЁй—ҙйҡҷпјҢеҚіжөӢйҮҸзҡ„й—ҙйҡҷеҮҸеҺ»иҙҹиҪҪеј•иө·зҡ„еј№жҖ§еҸҳеҪўгҖӮ
вҲҶ0В = вҲҶ1В - ПғFO
ПғFOеҜ№ж»ҡзҸ иҪҙжүҝеҫҲйҮҚиҰҒпјҢдҪҶеҜ№ж»ҡжҹұиҪҙжүҝж„Ҹд№үдёҚеӨ§пјҢеӣ дёәе®ғиў«еҒҮи®ҫдёәйӣ¶пјҢеӣ жӯӨвҲҶ0В = вҲҶ1гҖӮ
ж®ӢдҪҷеҶ…йғЁй—ҙйҡҷпјҲвҲҶfпјү
иҝҷжҳҜиҪҙжүҝе®үиЈ…еңЁиҪҙе’ҢеЈідҪ“дёҠд»ҘеҗҺзҡ„й—ҙйҡҷгҖӮеҝҪз•ҘдәҶз”ұиҪҙзҡ„иҙЁйҮҸеј•иө·зҡ„еј№жҖ§еҸҳеҪўгҖӮеҒҮи®ҫз”ұзҺҜпјҲеҶ…гҖҒеӨ–еңҲпјүиҶЁиғҖжҲ–收缩引иө·зҡ„й—ҙйҡҷеҮҸе°ҸдёәПғfпјҢеҲҷпјҡ
вҲҶf = вҲҶ0+Пғf
жңүж•ҲеҶ…йғЁй—ҙйҡҷпјҲвҲҶпјү
иҝҷжҳҜи®ҫеӨҮеңЁе…¶е·ҘдҪңжё©еәҰдёӢеӯҳеңЁзҡ„иҪҙжүҝй—ҙйҡҷпјҢдёҚеҢ…жӢ¬з”ұиҙҹиҪҪеј•иө·зҡ„еј№жҖ§еҸҳеҪўгҖӮиҝҷжҳҜеҸӘиҖғиҷ‘иҪҙжүҝй…ҚеҗҲПғfе’ҢеҶ…зҺҜ/еӨ–зҺҜд№Ӣй—ҙзҡ„жё©е·®Пғtеј•иө·зҡ„й—ҙйҡҷгҖӮиҪҙжүҝзҡ„еҹәжң¬йўқе®ҡиҪҪиҚ·д»…йҖӮз”ЁдәҺжңүж•Ҳй—ҙйҡҷвҲҶ=0гҖӮ
вҲҶ = вҲҶf вҖ“Пғt = вҲҶ0 вҖ“ (Пғf + Пғt)
е·ҘдҪңй—ҙйҡҷ(вҲҶF)
иҝҷжҳҜе®үиЈ…иҪҙжүҝ并еңЁиҙҹиҪҪдёӢиҝҗиЎҢж—¶зҡ„е®һйҷ…й—ҙйҡҷгҖӮеңЁиҝҷйҮҢпјҢеј№жҖ§еҸҳеҪўзҡ„еҪұе“ҚПғFдёҺй…ҚеҗҲе’Ңжё©еәҰдёҖиө·иў«еҢ…жӢ¬еңЁеҶ…гҖӮйҖҡеёёпјҢи®Ўз®—дёӯдёҚдҪҝз”Ёе·ҘдҪңй—ҙйҡҷгҖӮ
вҲҶFВ = вҲҶ + ПғF
жңҖйҮҚиҰҒзҡ„иҪҙжүҝй—ҙйҡҷжҳҜжңүж•Ҳй—ҙйҡҷгҖӮзҗҶи®әдёҠпјҢжңүж•Ҳй—ҙйҡҷвҲҶзЁҚеҫ®иҙҹзҡ„иҪҙжүҝдҪҝз”ЁеҜҝе‘ҪжңҖй•ҝгҖӮеңЁиҪҙжүҝиҙҹиҪҪзҡ„еҪұе“ҚдёӢпјҢзЁҚеҫ®иҙҹзҡ„й—ҙйҡҷпјҲжҲ–йў„иҪҪиҚ·пјүе°ҶеҸҳдёәжӯЈгҖӮ然иҖҢпјҢдёҚеҸҜиғҪдҪҝжүҖжңүиҪҙжүҝзҡ„й—ҙйҡҷиҫҫеҲ°зҗҶжғізҡ„жңүж•Ҳй—ҙйҡҷпјҢеҝ…йЎ»иҖғиҷ‘еҮ дҪ•й—ҙйҡҷвҲҶ0пјҢжүҚиғҪиҫҫеҲ°йӣ¶жҲ–з•Ҙиҙҹзҡ„жңүж•Ҳй—ҙйҡҷжңҖе°ҸеҖјгҖӮдёәдәҶи®Ўз®—иҜҘеҖјпјҢйңҖиҰҒзҹҘйҒ“з”ұеҶ…еңҲе’ҢеӨ–еңҲзҡ„иҝҮзӣҲпјҲй…ҚеҗҲпјүDfеј•иө·зҡ„й—ҙйҡҷеҮҸе°ҸйҮҸпјҢд№ҹйңҖиҰҒзҹҘйҒ“з”ұеҶ…еңҲе’ҢеӨ–еңҲд№Ӣй—ҙзҡ„жё©е·®Dtеј•иө·зҡ„й—ҙйҡҷеҸҳеҢ–гҖӮ
е®үиЈ…еҗҺж®ӢдҪҷеҶ…йғЁй—ҙйҡҷзҡ„и®Ўз®—
еҪ“иҪҙжүҝеҶ…еңҲеҺӢй…ҚеҗҲеҲ°иҪҙдёҠж—¶пјҢжҲ–еҪ“еӨ–еңҲеҺӢй…ҚеҗҲеҲ°еЈідҪ“дёӯж—¶пјҢз”ұдәҺиҪҙжүҝж»ҡйҒ“зҡ„иҶЁиғҖжҲ–收缩пјҢеҫ„еҗ‘еҶ…йғЁй—ҙйҡҷиҮӘ然дјҡеҮҸе°ҸгҖӮдёҖиҲ¬жқҘиҜҙпјҢеӨ§еӨҡж•°жіөйғҪжңүдёҖдёӘж—ӢиҪ¬иҪҙпјҢиҰҒжұӮеҶ…еңҲе’ҢиҪҙд№Ӣй—ҙзҙ§еҜҶй…ҚеҗҲпјҢеӨ–еңҲе’ҢеӨ–еЈід№Ӣй—ҙжқҫж•Јй…ҚеҗҲгҖӮеңЁиҝҷдәӣжғ…еҶөдёӢпјҢеҸӘйңҖиҰҒиҖғиҷ‘иҝҮзӣҲй…ҚеҗҲеҜ№еҶ…еңҲзҡ„еҪұе“ҚгҖӮ
е…¬ејҸ1дёӯжҳҫзӨәдәҶ6310еҚ•еҲ—ж·ұжІҹзҗғиҪҙжүҝзҡ„зӨәдҫӢи®Ўз®—гҖӮжүҖдҪҝз”Ёзҡ„иҪҙе…¬е·®дёәK5пјҢиҖҢеЈідҪ“дёәH7 - иҪҙжүҝеҶ…еңҲйҮҮз”ЁиҝҮзӣҲй…ҚеҗҲгҖӮ
е…¬ејҸ1пјҡ
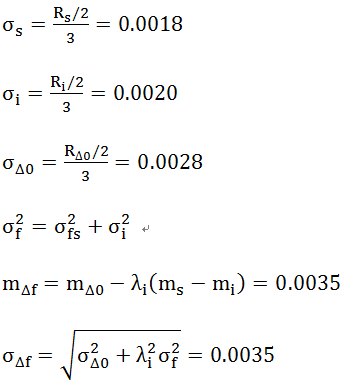
ејҸдёӯпјҢ
Пғs = иҪҙеҫ„зҡ„ж ҮеҮҶеҒҸе·®
Пғi = еӯ”еҫ„зҡ„ж ҮеҮҶеҒҸе·®
Пғf = е№Іжү°пјҲ收缩жҲ–иҶЁиғҖпјүзҡ„ж ҮеҮҶеҒҸе·®
Пғв–і0 = еҫ„еҗ‘й—ҙйҡҷзҡ„ж ҮеҮҶеҒҸе·®пјҲе®үиЈ…еүҚпјү
Пғв–іf = ж®ӢдҪҷй—ҙйҡҷзҡ„ж ҮеҮҶеҒҸе·®пјҲе®үиЈ…еҗҺпјү
ms = иҪҙзӣҙеҫ„е№іеқҮеҖјпјҲПҶ50+0.008пјү
mi = еӯ”еҫ„е№іеқҮеҖјпјҲПҶ50-0.006пјү
mв–і0 = еҫ„еҗ‘й—ҙйҡҷе№іеқҮеҖјпјҲе®үиЈ…еүҚпјҢ0.014пјү
mв–іf = ж®ӢдҪҷй—ҙйҡҷе№іеқҮеҖјпјҲе®үиЈ…еҗҺпјү
Rs = иҪҙеҫ„е…¬е·®пјҲ0.011пјү
Ri = иҪҙжүҝеҶ…еӯ”е…¬е·®пјҲ0.012пјү
Rв–і0 = еҫ„еҗ‘й—ҙйҡҷиҢғеӣҙпјҲе®үиЈ…еүҚпјҢ0.017пјү
О»i = з”ұиЎЁи§Ӯе№Іж¶үеј•иө·зҡ„ж»ҡйҒ“иҶЁиғҖзҺҮпјҲеҸӮиҖғеҖј0.75пјү
иҪҙзӣҙеҫ„гҖҒеӯ”еҫ„е’Ңеҫ„еҗ‘й—ҙйҡҷжҳҜж ҮеҮҶиҪҙжүҝжөӢйҮҸеҖјгҖӮеҒҮи®ҫ99.7 % зҡ„йӣ¶д»¶еңЁе…¬е·®иҢғеӣҙеҶ…пјҢеҲҷеҸҜд»Ҙи®Ўз®—еҮәе®үиЈ…еҗҺеҶ…йғЁй—ҙйҡҷпјҲж®ӢдҪҷй—ҙйҡҷпјүзҡ„е№іеқҮеҖјпјҲmвҲҶfпјүе’Ңж ҮеҮҶеҒҸе·®пјҲПғвҲҶfпјүгҖӮжөӢйҮҸеҚ•дҪҚдёәжҜ«зұіпјҲmmпјүгҖӮ
з”ұиЎЁи§Ӯе№Іж¶үеј•иө·зҡ„ж»ҡйҒ“иҶЁиғҖе’Ң收缩зҡ„е№іеқҮйҮҸз”ұО»iВ (mmВ вҖ“ mi)и®Ўз®—гҖӮ
дёӢејҸз”ЁдәҺеңЁ99.7 % зҡ„жҰӮзҺҮеҶ…зЎ®е®ҡе®үиЈ…еҗҺзҡ„еҶ…йғЁй—ҙйҡҷеҸҳеҢ–пјҲRвҲҶfпјүпјҡ
RвҲҶf = mвҲҶf Вұ 3ПғвҲҶf = + 0.014иҮі- 0.007
ж®ӢдҪҷй—ҙйҡҷзҡ„е№іеқҮеҖјпјҲmвҲҶfпјүдёә + 0.0035пјҢ6310иҪҙжүҝе®үиЈ…еҗҺзҡ„еҶ…йғЁй—ҙйҡҷиҢғеӣҙдёә- 0.007иҮі0.014гҖӮ
еҫ„еҗ‘еҶ…йғЁй—ҙйҡҷе’Ңжё©еәҰ
еҪ“иҪҙжүҝеңЁиҙҹиҪҪдёӢиҝҗиЎҢж—¶пјҢж•ҙдёӘиҪҙжүҝзҡ„жё©еәҰе°ҶеҚҮй«ҳпјҢиҝҷеҢ…жӢ¬ж»ҡеҠЁе…ғ件гҖӮдҪҶжҳҜпјҢз”ұдәҺиҝҷз§ҚеҸҳеҢ–еҫҲйҡҫжөӢйҮҸжҲ–дј°и®ЎпјҢеӣ жӯӨйҖҡеёёеҒҮи®ҫж»ҡеҠЁе…ғ件зҡ„жё©еәҰдёҺеҶ…еңҲжё©еәҰзӣёеҗҢгҖӮ
е…¬ејҸ2пјҡ

еҶҚж¬Ўд»Ҙ6310иҪҙжүҝдёәдҫӢпјҢеҸҜд»ҘдҪҝз”Ёе…¬ејҸ2и®Ўз®—з”ұеҶ…еңҲе’ҢеӨ–еңҲд№Ӣй—ҙ5в„ғзҡ„жё©е·®еј•иө·зҡ„й—ҙйҡҷеҮҸе°ҸгҖӮ
е…¬ејҸ3пјҡ
ж»ҡзҸ иҪҙжүҝпјҡDeВ = (4D + d) / 5
ж»ҡеӯҗиҪҙжүҝпјҡDeВ = (3D + d) / 4
е…¬ејҸ3з”ЁдәҺи®Ўз®—еӨ–еңҲж»ҡйҒ“зӣҙеҫ„гҖӮеҲ©з”ЁвҲҶfе’ҢПғtзҡ„и®Ўз®—еҖјпјҢжңүж•ҲеҶ…йғЁй—ҙйҡҷпјҲвҲҶпјүеҸҜз”ұдёӢејҸ4зЎ®е®ҡгҖӮ
е…¬ејҸ4пјҡ
D = DfВ вҖ“ dtВ = (+0.014 пҪһ -0.007) вҖ“ 0.006 = +0.008 пҪһ -0.013
еӣҫ2жҳҫзӨәдәҶжңүж•ҲеҶ…йғЁй—ҙйҡҷеҰӮдҪ•еҪұе“ҚиҪҙжүҝеҜҝе‘ҪпјҢеңЁжң¬дҫӢдёӯпјҢеҫ„еҗ‘иҪҪиҚ·дёә3,350 NпјҲжҲ–зәҰдёәеҹәжң¬йўқе®ҡиҪҪиҚ·зҡ„5%пјүгҖӮеңЁжңүж•ҲеҶ…йғЁй—ҙйҡҷдёә-13Ојmж—¶пјҢиҪҙжүҝеҜҝе‘ҪжңҖй•ҝгҖӮдјҳйҖүжңүж•ҲеҶ…йғЁй—ҙйҡҷиҢғеӣҙзҡ„дёӢйҷҗд№ҹдёә-13ОјmгҖӮ
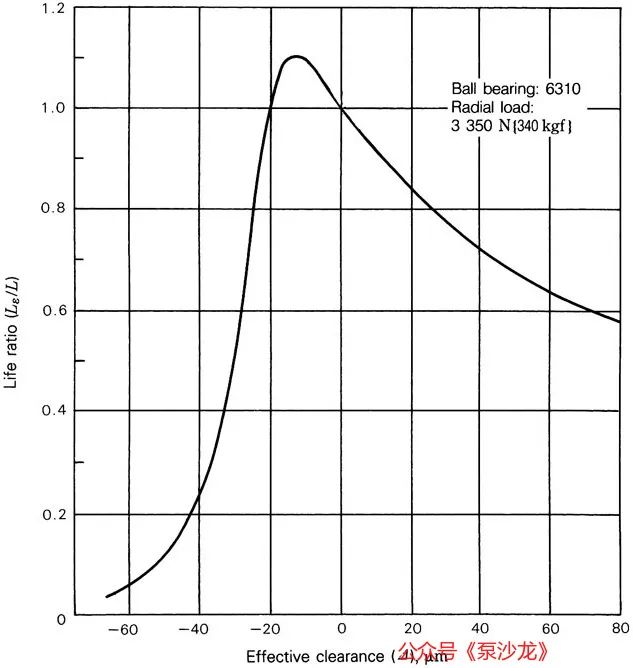
еӣҫ2пјҡ6310ж»ҡзҸ иҪҙжүҝжңүж•Ҳй—ҙйҡҷдёҺиҪҙжүҝеҜҝе‘Ҫзҡ„е…ізі»
еә”з”Ё
иҷҪ然еңЁзҗҶи®әдёҠпјҢд»ҘзЁҚеҫ®иҙҹзҡ„й—ҙйҡҷдёәзӣ®ж ҮжҳҜиҪҙжүҝеҜҝе‘Ҫзҡ„жңҖдҪійҖүжӢ©пјҢдҪҶеңЁе®һи·өдёӯпјҢи®ҫи®ЎжҲ–еҲ¶йҖ иҪҙжүҝеӨ„дәҺйў„еҠ иҪҪзҠ¶жҖҒзҡ„жіөж—¶еҝ…йЎ»е°ҸеҝғгҖӮ
еҰӮеӣҫ2жүҖзӨәпјҢеҜҝе‘ҪжҜ”зЎ®е®һеңЁ-13 Ојmж—¶иҫҫеҲ°еі°еҖјпјҢдҪҶйҡҸзқҖйў„еҠ иҪҪзҡ„еўһеҠ пјҢеҜҝе‘ҪжҜ”жҖҘеү§дёӢйҷҚгҖӮеҰӮжһңиҪҙжүҝйў„еҠ иҪҪиҝҮеӨ§пјҢдё”еҠ е·Ҙе…¬е·®жҲ–е·ҘдҪңжё©еәҰзҡ„дёҚжӯЈзЎ®пјҢйӮЈд№ҲеҫҲе®№жҳ“еҜјиҮҙеҜҝе‘ҪжҜ”йў„жңҹзҡ„иҰҒзҹӯгҖӮеҸҰдёҖж–№йқўпјҢиҝҮеӨ§зҡ„й—ҙйҡҷдјҡеҜјиҮҙиҪҙжүҝеҷӘйҹігҖҒж»ҡеҠЁе…ғ件жү“ж»‘е’ҢжіөжҖ§иғҪеҸҳе·®гҖӮеҝ…йЎ»ж №жҚ®еә”з”Ёзҡ„йңҖиҰҒеҜ№й—ҙйҡҷе’ҢиҪҙжүҝйў„еҠ иҪҪиҝӣиЎҢжқғиЎЎгҖӮ
дәҶи§ЈиҪҙжүҝеҶ…йғЁй—ҙйҡҷзҡ„йҮҚиҰҒжҖ§пјҢе°ҶжңүеҠ©дәҺеўһеҠ иҪҙжүҝеҜҝе‘Ҫ并дјҳеҢ–жіөзҡ„ж•ҙдҪ“жҖ§иғҪгҖӮ
дҪңиҖ…з®Җд»ӢпјҡTodd BrewerжҳҜNSKзҡ„еә”з”Ёе·ҘзЁӢеёҲгҖӮд»–жҜ•дёҡдәҺеҜҶжӯҮж №зҗҶе·ҘеӨ§еӯҰпјҢиҺ·еҫ—жңәжў°е·ҘзЁӢзҗҶеӯҰеӯҰеЈ«еӯҰдҪҚгҖӮд»–жңү18е№ҙзҡ„е·ҘзЁӢз»ҸйӘҢпјҢ11е№ҙеңЁиҪҙжүҝиЎҢдёҡе·ҘдҪңпјҢ6е№ҙеңЁNSKе·ҘдҪңгҖӮ



